| Вычисление числа |  |
|||||||||||||||||||||||||
ТЕМА
: Экспериментальное вычисление числа 
в опыте Бюффона. |
||||||||||||||||||||||||||
| ОПИСАНИЕ
: Оказывается, приближенно найти
можно с помощью иголки ... и теории вероятностей. Такой способ придумал
французский естествоиспытатель Ж. Л. Л. Бюффон (1707-1788). |
||||||||||||||||||||||||||
Для осуществления опыта Бюффона нужно немного : плоская горизонтальная поверхность с нанесенными на ней параллельными равноотстоящими прямыми и игла. Расстояние между прямыми H и длина иглы L должны удовлетворять соотношениию L < H. Будем произвольным образом подбрасывать иглу над такой поверхностью, сообщая ей каждый раз небольшое вращение так, чтобы игла свободно падала с некоторой высоты, составляя при падении совершенно случайный угол с начерченными прямыми. После каждого броска будем отмечать, пересекла или не пересекла игла одну из параллельных прямых и подсчитывать частоту пересечений, то есть отношение числа m бросаний, при которых пересечение произошло, к их общему числу n. Довольно скоро мы заметим, что при многократном повторениии бросаний частота будет меняться все меньше и меньше. Более того, если произвести много длинных серий подбрасываний, обнаружится, что частота пересечений почти во всех сериях будет примерно одной и той же. Эта частота будет равна вероятности р того, что игла пересечет одну из линий. Ведь вероятность - это как раз и есть то значение, около которого колеблется частота осуществления того или иного события в достаточно длинных сериях экспериментов. Методы теории вероятностей позволяют исходя из условий проведения эксперимента рассчитывать вероятности теоретически. Вероятность пересечений р в опыте Бюффона будет равна
А поскольку частота пересечений m/n примерно
равна этой вероятности, для приближенного вычисления
|
||||||||||||||||||||||||||
| УПРАВЛЕНИЕ осуществляется с помощью кнопок : БРОСОК, НАЗАД, кнопки подсчета числа пересечений ПЛЮС. | ||||||||||||||||||||||||||
|
ЗАДАНИЕ : Проверка
формулы (*). Провести длинную серию экспериментов по подбрасыванию иглы.
Подсчет числа бросков n проводится автоматически.
Подсчет числа пересечений m необходимо проводить
вручную с помощью кнопки ПЛЮС. Используя полученные в эксперименте значения
n, m и принимая L = 60 мм,
H = 80 мм , рассчитать по формуле (*) приближенное
значение числа . Сравнить
полученные значения с результатами лучших <<игроков>>, приведенными
ниже. |
||||||||||||||||||||||||||
| Лучшие <<игроки>> | ||||||||||||||||||||||||||
| В
19 веке, когда теория вероятностей рассматривалась как полуэкспериментальная
наука, такие опыты имели большое значение и весьма тщательно ставились
многими учеными. Ниже приводится таблица, взятая из курса теории вероятностей
Б.В. Гнеденко. В первой колонке даны фамилии ученых , бросавших иглу,
во второй - год проведения опыта, в третьей - число бросаний, из которого
было определено , и в последней
- полученное в результате опытов значение. В нижней строке таблицы дано
значение с восемью знаками. |
||||||||||||||||||||||||||
|
||||||||||||||||||||||||||
Дополнительное задание : 1)Вывести формулу (*), |
||||||||||||||||||||||||||
| 2)
Доказать , что в опыте Бюффона нельзя получить значение
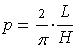с точностью указанной Лаццирини. |
||||||||||||||||||||||||||
.
.
(*)